Bienvenidos

Sean todos bienvenids a opinar y aprender en  nuestro blog,esn este blog veran temas asociados a geometria
como Elementos y Angulos de una Circunferencia, teoremas de esta y ejemplos variados.

ELEMENTOS DE LA CIRCUNFERENCIA

CUERDA:Es un segmento que une dos puntos de la circunferencia.:

    DIAMETRO : Es la Cuerda que pasa por el centro de la circunferencia

ARCO:Cuando cada una de las partes en que una cuerda divide a la circunferencia,se suele asociar a cada cuerda el menor arco que delimita.     

.      

          SEMICIRCUNFERENCIA: ES  Cada uno de los arcos iguales que abarca un diámetro. 

 

ANGULOS DE LA CIRCUNFERENCIA

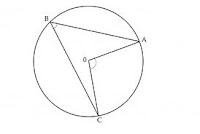
ANGULO CENTRAL:El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.

 

ANGULO INSCRITO:El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.

ANGULO SEMIINSCRITO: El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.

 

ANGULO INTERIOR:Su vértice es interior a la circunferencia y sus lados secantes a ella.Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

         

Ángulo exterior

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:

                                  

TEOREMA DE CIRCUNFERENCIA

Teoremas fundamenTales - Trazos

 

-Teorema de las tangentes

-Teorema de las cuerdas

-Cuadrilátero circunscrito a una circunferencia

-Teorema de las secantes

-Teorema de la tangente y la secante

La suma de los ángulos de cualquier triángulo e menor de 2d.

Examinemos primeramente eL triángulo rectángulo ABC (figura 30). Sus lados a , b , c se exponen, respectivamente, en forma de un segmento de la perpendicular euclidiana a la recta u , de un arco de la circunferencia euclidiana con el centro M y de un arco de la circunferencia euclidiana con el centro N . El ángulo C es recto. El ángulo A es igual al ángulo entre las tangentes de las circunferencias b y c en el punto A o, lo que es lo mismo, al ángulo entre los radios NA MA de estas circunferencias. Por último, ∠ B = ∠ BNM. y

 

 TEOREMA DE LAS CUERDAS
Si 2 cuerdas se interceptan en el interior de la circunferencia, el producto de los segmentos determinados en una cuerda es igual al producto de los segmentos determinados en otra cuerda.




 NP·PQ = RP·PS

TEOREMA DE LAS SECANTES

Si 2 rectas secantes interceptan a una circunferenia, el producto entre el segmento exterior a la circunferencia con el segmento totalen una de las secantes es igual al producto de los correspondientes segmentos en otra secante.




MP·SP = RP·QP

TEOREMA DE LA SECANTE Y LA TANGENTE
Si desde un punto exterior a una circunferencia, se traza una tangente y una secante, el cuadrado del segmento tangente equivale al producto entre el segmento exterior y el segmento total de la recta secante.

TP² = RP· QP